More on Mixture of Experts models
6 papers on different routing mechanisms
This is a follow up article to one I wrote at the beginning of August. That article was a discussion of Mixture of Expert models, and dove into how they work at a high level. After writing it, I had a lot of people suggesting more MoE papers to read, so I decided to do that. This article is a summary of 6 papers that explore different routing techniques, and cover a broad swath of the research landscape.
Routing techniques
There are several broad families of routing techniques:
Fully differentiable techniques, where the routing layer is but one layer in the network (although typically much smaller than the actual transformer blocks), and
Linear programming techniques, where the routing layer solves an isolated optimization problem.
Non-parametric approaches, e.g. hashing, which don’t solve or learn anything. These are mostly used for benchmarking.
Most research that focuses on high performance (as in, models that are good at modelling language) focus on either #1 or #2. The trend recently has been to focus on fully differentiable techniques, but it’s not clear to me how much that’s supported by the results, vs a decision that’s supported by the bias that most researchers have towards end-to-end learning (which, itself, is supported by research results from other domains, such as deep RL).
There are six papers that I will discuss in this post:
RL routing, which focuses on the underlying theory allowing us to back-propagate through stochastic neurons, but which doesn’t propose a specific method. This is included because it’s cited by most subsequent papers.
Non-parametric hash layers, which randomly comes up with a fixed token ↔ expert assignment once, and uses that indefinitely. The hash layers serve as a strong baseline, but probably shouldn’t be used in production.
BASE, which solves a linear assignment problem to allocate tokens to experts.
Differentiable Select-K, which is a fully differentiable version of the standard sparsely gated MoE layer.
Expert choice routing, which reverses the standard “token choice” framework where tokens choose the top expert for them to be routed to, and instead has each expert choose the top K tokens for it to see.
Soft MoE, which sends all tokens to every expert and combines the results with weights which are learned on a per-token basis.
This isn’t an exhaustive literature review, but is an attempt at summarizing the papers that one would want to read to get close to the state of the art if one were planning to implement a MoE system. If you haven’t read my previous MoE post, I’d encourage you to do that first.
RL routing
This paper is ancient (it’s from 2013!) but provides a lot of the background for using RL to route MoE models. They examine a question of how to estimate the gradient of a loss function with respect to the input of stochastic/hard non-linear neurons, as we can’t naively backprop through them. This is a problem which arises in the MoE work— see, for instance, the soft MoE paper later on, which has a solution to this as a key selling point.
The core idea is that it is possible to obtain estimated gradients by introducing small random perturbations in the system and observing the effects— the definition of the derivative!
We can numerically approximate this! Doing this naively is inefficient, as independently perturbing N parameters is Nx more expensive, but if we randomly introduce stochasticity in a way so that gradients can sometimes flow, we can then backprop in the standard way and adjust the neurons accordingly. The example is dropout— it also introduces a hard non-linearity with some probability, but we can still backprop through it without issue when the parameter is not dropped out. In the paper, they consider equations of the form
where a_i is an input, typically the output of other neurons, and z_i is a random variable. They consider 3 options:
The noisy rectifier:
\(h_i=\max(0,z_i+a_i),E[z_i]=0, h_i= \max(0,z_i+a_i), E[z_i]=0\)The STS unit (Stochastic Times Smooth):
\(h_i=b_i \cdot p_i, p_i=f(a_i), b_i \thicksim \text{Binomial}(p_i),\)
where f is some activation function (they use the sigmoid),
The Straight-Through Estimator, where you back-propagate through the hard threshold function as it was the identity. For instance, if we have the function
then using the ST estimator we’d set the gradient as
The ST estimator works quite well in practice:
It significantly outperforms the other stochastic methods when used to train a model to classify MNIST. It’d be nice to see more experiments to validate these models better; MNIST isn’t particularly compelling now, although this does date back to 2013.
The paper is interesting mostly for context into how we can actually train routing layers for MoE models.
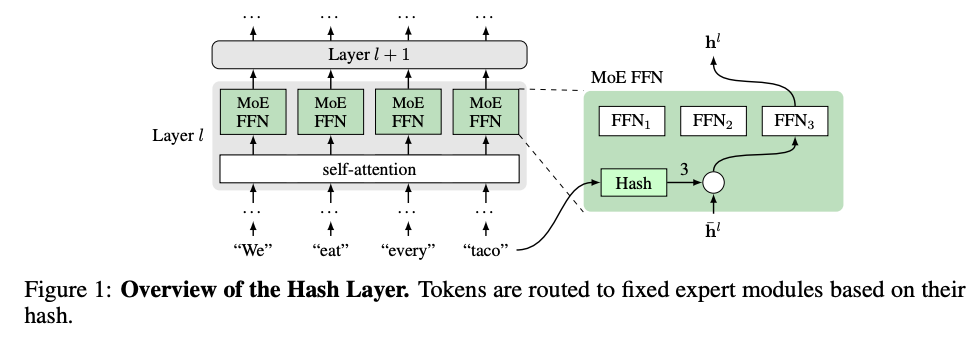
Non-parametric Hash layers
This is a paper I’m revisiting, as I had previously read it while reading Unified Scaling Laws for Routed Language Models. Intuitively, it doesn’t make sense to me that a non-parametric approach would perform comparably to a learned approach, so I find this paper compelling, as it demonstrates that a simple non-parametric model can approach the performance of learned models. This mirrors my experience as an AI poker researcher: UniformRandom (literally just picking a random bet) was a surprisingly hard benchmark for our learned agents to beat, and in certain subgames of e.g. Scotland Yard, was optimal. I continually found this fact surprising.
The method itself is quite simple:
In it, the tokens are hashed into a fixed number of buckets, each corresponding to an expert. The routing function uses the original input token rather than the hidden state, so there is no learning happening in the routing layer. As a result, the routing mechanism is fast, deterministic, and robust.
The authors consider a wide variety of hashing functions:
Random Hash, where they build a lookup table assigning every token to a fixed, random expert.
Balanced assignment, in which they build a lookup table which greedily assigns the most frequent tokens to the emptiest buckets. This is more balanced than Random Hashing, but still not perfectly balanced.
Bigram Hash, which hashes the current and previous token,
Previous Token Hash, which uses the previous token only,
Position Hash, hashing based on the position in the sequence
Oracle Future hash, used as a baseline, which hashes the next token,
Predicted Future Token Hash, which predicts the next token, and hashes over the prediction
Clustered Hashes, in which they obtain clusters using k-means over token embeddings from a baseline model, and assign experts to clusters
Dispersed hashes: which assigns similar tokens to different buckets, by using the same k-means clusters as Clustered Hashes, but distributing all tokens within each cluster equally across buckets.
A MultiHash layer is also used, in which the authors take N hashing functions, split the token embedding into N segments, and use each function to allocate each embedding segment to a different expert.
The hashing results are surprisingly good:
Their ablations also reveal that the sparse models they try (Hash/Switch) outperform the dense Baseline model they train, as well as the Wider Transformer (755M params). But the Deeper Transformer (also 755M) they train is better than the sparse models. This is interesting; a bunch of the scaling laws paper found that network architecture didn’t really matter, which isn’t consistent with my experience, so it’s nice to see that validated in the experiments here.
They also compare to BASE layers (which we will discuss later in this article), as shown in the plot on the right, and show an improvement. I’m surprised by this; I would have expected BASE layers to do strictly better, as they’re solving a linear programming problem. My suspicion is that the expert embeddings they use aren’t very good. The Hash Layers are significantly more performant than the BASE layers, as BASE requires two all-to-all communications, which are expensive.
In their ablations, they find that increasing the number of routing modules increases the advantage that Hash has over Switch. Their hypothesis is that with a small number of routers, learning to route is more important, but this advantage goes away quickly.
They experiment with all of the different hashing methods, and find that Balanced Assignment is the best (other than the Future token Oracle):
The other one that is roughly as good is Dispersed Hash, which randomizes tokens within each cluster across all the experts, making it effectively a more complicated randomization. This makes sense; from what I’ve seen reading routing papers, the most important characteristic is that tokens are balanced across experts so that the experts are trained well.
They perform a comparison on Wikitext-103, which finds that with a smaller BPE dictionary, the Hash layer does better than a Switch Transformer:
I suspect this is due to token balancing (or rather, unbalanced tokens). With a smaller BPE dictionary, I suspect the switch transformer struggles to balance the tokens, which the hash layer does by construction.
When they add in multiple hash functions, performance slightly increases, but not at a level that seems worth the complexity to me:
Generally, I’m surprised by this paper. It’s remarkable how well the method does. This should be used as a baseline for routing papers.
BASE
This paper introduces an algorithm called balanced assignment of experts (BASE) which focuses on formulating the problem of allocating tokens to experts as a linear assignment problem, which allows to use linear programming to find an optimal solution that guarantees each expert receives an equal number of tokens. By using a classical optimization approach, the method doesn’t introduce any new hyperparameters or auxiliary losses, and thus doesn’t add any complication to training. An implementation was released in Fairseq, FAIR’s sequence modeling toolkit.
In BASE, a single expert is assigned per token, in a way that maximized token-expert similarities. Expert specialization is learned by training a modified residual connection that mixes in each expert.
During training, the authors maximize model throughput by assigning an equal number of tokens to each expert. At test time, they assign each token to its highest scoring expert (”tokens choice”). They solve the following problem to assign tokens to experts (where we have T tokens, h_t is the representation of token t, we have E experts each with an associated embedding w_e, and we have an assignment index assigning tokens to experts 0 ≤ a_t ≤ E):
This objective function seeks to maximize the similarity of the token and expert embeddings while respecting the constraint that all experts receive an equal number of tokens.
To minimize the computational cost to solve this problem, which requires solving this for ET tokens across all the workers, the problem is decomposed by having each worker solve a separate assignment problem over the inputs it receives. Each worker then sends T/E tokens to each other worker. However, this is heavily correlated, because the tokens assigned to each worker during training are typically from the same domain. To enable specializing, they add a random routing step, where each worker sends an equal number of each tokens to each other worker randomly. In effect, the algorithm has three steps during training:
Each worker sends T/E tokens to each other worker randomly.
Each worker solves a separate linear assignment problem and routes T/E tokens to each expert.
At test-time, the workers simply assign each token the best expert. The hope is that the workers have learned a reasonably balanced assignment.
They find that their approach outperforms other sparse MoE models:
They also find that their approach matches the Sparsely Gated MoE model despite being simpler.
When it comes to compute efficiency, the best is (unsurprisingly) data parallel, but BASE is the second fastest approach due to the lower amount of communication needed between workers.
Routing layers that solve linear programming problems, like BASE, seem like a strong approach. They seem to have fallen out of fashion, which I don’t understand. I think that more people deploying MoE models would do well to consider LP-based approaches.
Note: This paper was built on with the Unified Scaling Laws for Routed Language Models paper, which proposed a variant: Sinkhorn-BASE. I won’t discuss it here, but it’s worth reading. It has a better matching step than BASE and, as a result, slightly improved performance.
Differentiable Select-K
This is a continuously differentiable sparse gate for MoE routing. The standard MoE routing problem is to select the best k out of n experts for each token. This is a constrained optimization problem, which isn’t optimized for the accelerators that handle contemporary ML workloads. This paper reformulates the problem to use an unconstrained formulation that is equivalent to the original problem. The reformulation uses a binary encoding scheme to implicitly enforce the cardinality constraint. By using a binary encoding, the number of parameters used by DSelect-k is logarithmic in the number of experts, while existing gates (e.g. the Sparse MoE gate) are linear. This could be useful with techniques like soft MoE (discussed later) which have a massive number of experts.
The authors propose two varieties: per-example, in which each token chooses an expert, and static, in which a weighting of experts is chosen once and does not vary per input. The static routing is not standard and is rarely used in the literature; it is more analogous to an ensembling technique. The only other time I’ve come across a similar problem is in the random hashing paper.
The authors compare DSelect-k to Top-k. The Top-k gate is defined by
where the TopK function is equal to the identity for the top k elements, and -∞ for the rest. While not continuous, Top-k allows for gradient propagation for the TopK outputs (using the “straight-through” method introduced in the RL routing paper discussed earlier).
The authors conducted an auxiliary experiment to show why continuity is a desired behaviour. In it, they used a MoE model to generate synthetic data, and trained routing layers to learn which experts were used to generate which data. They find that DSelect-k is able to recover the true experts, while TopK is not; additionally, the weights chosen by DSelectK are much more well behaved, while those from TopK exhibit a weird oscillatory behaviour, which the authors attribute to the discontinuous nature of the TopK router:
The authors conduct training on the MovieLens dataset, with two tasks: 1) a binary classification problem predicting whether a user watches a particular movie, and a regression problem to predict the rating a user assigns a given rating. They plotted the expert weights during training, and TopK has much higher variance in the weights, where the weight assigned to a given expert abruptly changes:
What I find interesting about these results is that these auxiliary metrics show a large degree of variance, which one would expect to be quite harmful in the final performance. However, DSelectK does not radically differ in final performance compared to the other routing functions.
That surprises me; given the high degree of variance induced by the discontinuous nature of the function, I’d expect to see more instability. Perhaps this is due to the fact that the authors don’t train a LLM; it would be interesting to see an ablation where the authors train a LLM. I would expect fewer loss spikes and more stability during training from a smoother function like DSelectK. That would be prohibitively expensive, as all things LLM are.
Expert choice routing
A one sentence summary of this paper would be: “Learns the greedy top-k tokens per expert.”
Load imbalance is a major problem in MoE models. Often, we see the top experts get more tokens than the rest, which tends to compound over time. As a result, many papers dedicate a lot of time & effort to balancing the load across experts.
This paper seeks to address that by having experts select the top-K tokens for them to see, rather than having tokens select the top-K experts, as has been previously done.
This has the advantage that tokens can be seen by a variable number of experts. Their model outperforms the T5 dense model in 7/11 tasks; I would like to see stronger performance, as my bias is that a model that is exactly as good as T5 would outperform it in 5.5/11 tasks (50%), and 7 is not significantly larger than 5.5.
Generally speaking, I’m suspicious when any method demonstrates an improvement over an existing method, because most researchers tend to tune their new method better than the old one. This is human nature; “it is difficult to get a man to understand something, when his salary depends on his not understanding it.” As such, I want to see the new method be heads-and-shoulders better than the previous one if they’re claiming improvement. My bias is that, with access to the amount of GPUs that a typical Google researcher has, I could show an improvement in most deep learning techniques simply by doing more hyper-parameter tuning. If I had the ability to add an arbitrary technique to it, that introduced more hypers, I could do better still.
Having said that caveat, the paper does intuitively make sense: in most token—choice routing models, each token is seen by exactly k experts, and thereby uses the same amount of compute. This is sub-optimal! We’re effectively offloading all compute allocation decisions to the tokenizer, which is often extremely simple (e.g. byte pair encoding). Methods which can allocate more compute to certain tokens should be significantly better.
An advantage that this technique has is latency: in token-choice methods, where each token chooses the top-K experts to be routed to, some experts will receive more tokens than others, causing step latency to be bottlenecked by the most loaded expert. To get around this, some implementations (e.g. the OLNN paper tried this in some of the appendix experiments) force equal allocations, but this is unwieldy and also harms latency, as the top-K function isn’t a good fit for the programming model used by accelerators (they’re good at matmuls, not sorting). However, this technique requires solving an integer linear program to allocate the tokens, which can be a nightmare itself; they use an approximation to allow it to run on TPUs.
Soft MoE
I’ve saved, perhaps, the best (or at least most novel) paper for last. Unlike most other MoE models, which use the routing layer to discretely route tokens to experts, Soft MoE passes different weighted combinations of all tokens to each expert. The standard sparse MoE transformer has to solve a discrete optimization problem, which is difficult to optimize due to differentiability. By making this a soft combination, it is immediately differentiable.
In the Soft MoE algorithm, they have a batch of m tokens which we refer to as X. They have n experts, each expert with p slots, and we use Φ to refer to the parameters for the experts (a d x (n * p) matrix). The input slots to the MoE layer, X’, is the weighted combination of X:
The matrix D is just the output of softmaxxing over the columns of XΦ. We call the p-th expert over the corresponding rows of X’:
And then compute the output tokens, Y, with a softmax over the rows:
The output of softmaxxing over the rows is called the combine weights, while the output of softmaxxing over the columns is called the dispatch weights.
This formulation has several nice properties:
It is fully differentiable. There are no nasty discrete functions to kill the gradients.
Token dropping isn’t an issue, like it is with the top-K router from the OLNN paper (discussed in a previous edition), as every slot is filled with a weighted average of all tokens, and the weights are strictly positive thanks to the softmax.
It’s fast, as it avoids sorting/top-k operations, which are slow on accelerators (particularly TPUs).
A major disadvantage is that it doesn’t currently work with auto-regressive decoders, i.e. all generative LLMs.It shouldn’t be particularly difficult to extend it, but it will require additional (careful) work.
They compare their method to the tokens choice (where every token selects the top-K experts with the highest routing score) and experts choice (where every expert selects the top-C tokens in terms of routing score) routing techniques. The results are quite strong, with soft MoE performing distinctly better in the two image tasks they study:
It also performs better when compared against ViTs with similar FLOPS:
They perform a number of ablations, and find that:
The optimal number of slots per expert is small: 1 or 2.
The optimal number of experts is roughly the same number as the amount of input tokens
What I find particularly compelling about this model is that it removes the complexity of sparse models.
I’m curious about the potential to make a router that has the flexibility to learn the slots though; something that could interpolate between this and the standard expert/token choice MoE routing models seems compelling.
Some conclusions
My take away from reading these papers was:
More papers should use hash layers as a benchmark.
It’s not clear to me that differentiability matters much. It seems intuitively nice to have, but I wouldn’t really give up anything else to get it.
Soft MoE doesn’t seem completely ready for production— the optimal number of slots per expert being 1 or 2 seems prohibitively expensive— but I think that an approach like this is the future, as I suspect that the performance benefits will continue to grow as more researchers explore soft routing techniques.
If I were actively focusing on MoE research, I would be looking into combining these, and looking at a fully differentiable, expert choice, soft routing layer. It seems fairly straightforward to combine these, and I suspect the advantages would stack.
Linear programming routing, while it performs strong, adds a lot of complexity to the stack. I’m not convinced that it’s really worth this complexity. However, the performance is strong, so it is worth benchmarking.














This is great!