How does batching work on modern GPUs?
The first and most important optimization you can do for any modern deep learning system, generally speaking, is to implement batching. When you batch inference, instead of sending a single input, you send a batch of N inputs. Most of the time, depending on the specific value of N, this is free— running inference takes the exact same amount of time with a single example as it does with N examples. Why is this? At first, it seems like processing the batch shouldn’t be free— after all, Nx more work is being done.
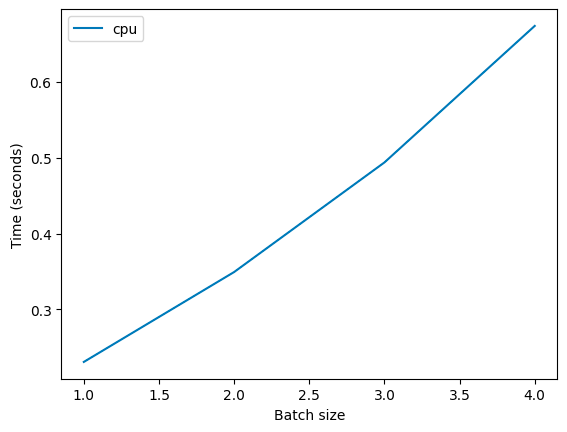
And with a naive model of how neural networks work, it isn’t free. The batched calculation requires Nx the compute to run, and, in fact, if you run this on CPU, you’ll see that this is true (average inference time for ResNet50, Colab):
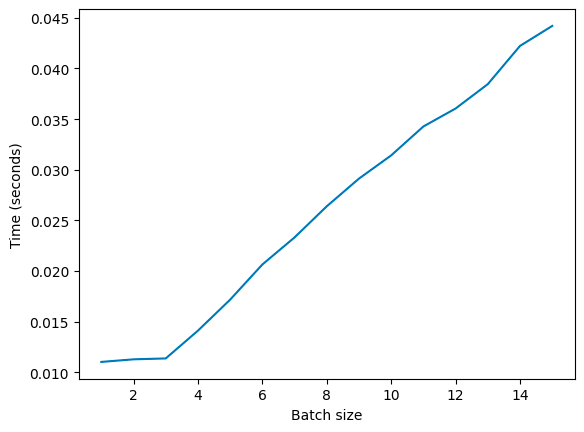
However, when you run the same example on a modern GPU, this isn’t the case. This is what we see (on a T4):
Going from a batch size of 1, to 2, to 3 requires no additional time, and then after that it increases linearly.
Why is this? Concurrency. Modern GPUs run their operations concurrently (and are, actually, slower than CPUs on a per-thread basis).
When we think of “calculating inference for an example with a model”, we typically think of the model as a single block, when, of course, it’s made up of many matrices. When we run inference, each matrix is loaded into memory. Specifically, each block of the matrix is loaded into on-device memory, namely the shared memory unit (only 192kb big on an A100). The block is then used to compute the results for every element in the batch. Note that this is not the same as GPU RAM, i.e. HBM. An A100 has 40GB or 80GB of HBM depending on the model, but only 192kb of on-device memory. This creates a memory bandwidth bottleneck when performing mathematical operations, as we are constantly moving data in and out of the on-device memory. We can approximate the time it takes to transfer the weights by calculating the model size / memory bandwidth ratio, and approximate the time it takes to do the calculation by model FLOPS / GPU FLOPS.
With an MLP, the FLOPS are approximately 2 * the number of parameters * the number of elements in the batch (2 * m * n * b for a batch size of b and a m x n matrix). As a result, the transfer time is equal to the calculation time when
Note that we can cancel out the number of parameters here:
And rearrange in terms of the batch size:
When the batch size is less than the ratio of FLOPS to memory bandwidth, we are bottlenecked by memory bandwidth. When it is more, we are bottlenecked by FLOPS. Note that this analysis is for a MLP, not for a convolutional network, like ResNet50. That gets a bit trickier.
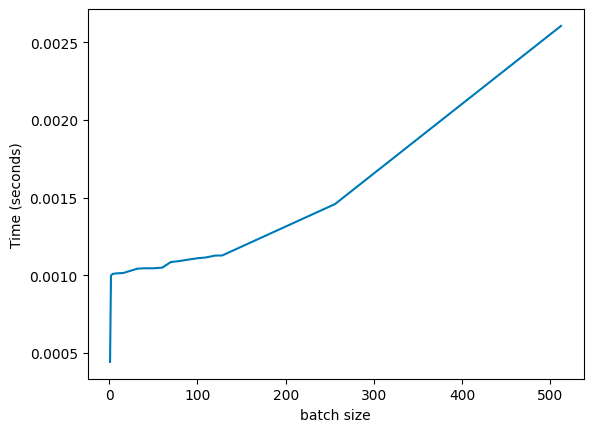
On a T4 GPU (datasheet), we have 65 TFLOPS of fp32, and 300 gb/s of memory bandwidth, so the magic ratio should be 216. When we run a MLP (depth: 8, width: 1024), we see roughly what we’d expect:
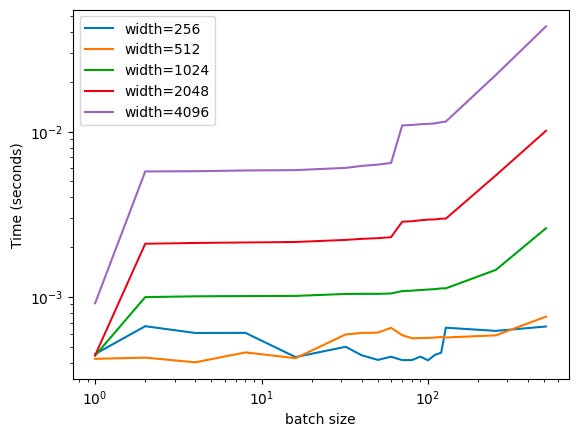
There’s some noise, but it’s basically what we’d expect: inference time starts increasing dramatically around the ~128 mark (here, we double the batch size, so we see batches at 128, 256, and then 512). And, if we vary the width of the MLP layers, we see this is true across a broad variety of architectures (the following is a log-log plot, to fit everything in):
This is pretty cool! We can see the critical threshold across a broad variety of different architectures. What’s also interesting is that the smaller networks don’t really see any scaling, taking roughly constant time across the entire range of batch sizes (from 1 to 512). My hand-wavy explanation for this is that this is because GPUs are really, really fast when it comes to actually doing math, but everything else (CPUs, etc.) is kinda slow. We see a ton of noise at the start, which I don’t have a great explanation for (other than shrugging and saying “overhead”).
For many ML engineers, their time isn’t spent doing much machine learning, but rather it’s spent just getting rid of overhead, which is typically in the non-ML code. In reinforcement learning (RL) research, particularly for researchers who work on continual learning problems, where there’s a single agent taking a long stream of actions, it’s often not worth it to use a GPU for experiments unless either 1) you have a very large network or 2) you extensively optimize every other aspect of your stack (if you want to make an old DeepMind engineer squirm, ask them about in-graph environments— at one point, we were implementing RL environments within the tensorflow graph).
What about convolutional networks?
In a convolutional network, the weights are equal to the number of filters times the filter size. For torch.nn.Conv2d , this is kernel_size^2 * out_channels. So if we have a (224, 224) image with a stride of 1 and a kernel size of 3, we apply the same filter 224 times. This means that, basically, for a convolutional layer, there’s much less advantage to batching, as we’re reusing the same weights many, many times. For a pooling layer, it’s basically linear in the number of pixels, as you’d expect.
What about transformers?
Transformers are basically just MLPs, so we can treat them as the same. They have an attention mechanism, obviously, but with a KV cache (which keeps the computed data around in memory), the time taken by attention is minimal. I wrote about this a lot previously.
The same is true for a Mixture of Experts model. In many transformer implementations, the KV cache lives inside the attention class (e.g. MaxText is a great example). As the only difference between a MoE model and a vanilla decoder is that some of the feedforward layers are replaced with MoE layers, the KV cache will behave the same, as will inference, with one wrinkle.
The wrinkle is that the gating mechanism in a MoE layer will split the batch across experts, so if the gate doesn’t split the batch uniformly, this can cause problems. There are different routing mechanisms which avoid this (e.g. expert’s choice) but in autoregressive decoders, you’re pretty much forced to only use token’s choice, which has a tendency towards biased gates. Forcing the gate to evenly allocate tokens is 1) an area of active research and 2) an important goal that is optimized during training.
I hope this has been helpful— please reach out if you have any batching questions (or, more importantly, any corrections).


Hey Fin, I know being a Dad must be crazy, but are you going to continue this Newsletter?
hi, why magic number is 216 ? 65TFLOPS / (2 * 300gb/s) = 108