Transformer inference tricks
How to make your model run faster than a greased pig
Transformer inference tricks
Special thanks to @cis_female for discussing the intricacies of sparsity with me, and @nostalgebraist for correcting an error in the quantization section; I now think that the evidence shows that quantizing, at least to 4 bits or more, has a very minimal tradeoff in terms of performance.
I’m going to discuss a number of optimizations that can be done to make inference for transformers either faster or more efficient.
KV Cache
By far the most common (and most important) optimization for a decoder is a KV cache. In a decoder model, the keys and values will be identical for the prompt for every iteration of decoding. Moreover, once you’ve ran a token through, the keys and values will be the same for that token for every subsequent iteration. As a result, you can cache the prompt, and incrementally add the KV tensors for each token to the cache as they are decoded. Doing so removes a lot of compute. Inside the attention mechanism, we’re able to go from multiplying two tensors of shape (batch, context_length, feature_dim) to multiplying a query tensor of shape (batch, 1, feature_dim) with your KV tensors of shape (batch, context_length, feature_dim). Consequently, sampling is no longer quadratic in complexity, allowing us to get decent decoding (sampling) performance with longer context lengths.
In practice, this causes added complexity inside your implementation, as you now have state rather than just running pure functions, so you have to keep running inference for the same sequences, even if one is done (see, eg, the Google MaxText implementation).
The KV cache requires 2 * n_layers * n_heads * d_head parameters. For GPT-3, with n_layers = 96, n_heads=96, d_head = 128, this would require 2.4M parameters for every token in your context. With typical 16-bit precision, this would require 5MB per token; if you have a context window of 2048 tokens, that’s 10GB of HBM dedicated to your KV cache. Expensive, but not outrageous. And well worth every GB.
These memory requirements are a big part of the reason why it’s so hard to use consumer grade GPUs for LLMs— the most powerful consumer card is the 4090, which has only 24GB of HBM. It has FLOPS that are comparable to the enterprise grade chips, but the memory limits are much lower, making it difficult to fit the weights and the KV cache into memory.
Speculative decoding
Speculative decoding is a technique that is used when you have excess compute capacity, typically in the local inference setting. It exploits the property of modern accelerators whereby it takes the same amount of time to run inference on a batch of data as it does to run inference on a single datapoint. For an A100, for instance, you can run inference on up to 160 datapoints in the same amount of time as a single datapoint. As a result, many techniques have cropped up to exploit this, such as beam search, MCTS, or speculative decoding.
In speculative decoding, one has two models: a small, fast, one, and a large, slow one. As the inference speed for a modern decoder is directly proportional to the number of parameters, with a smaller model, one can run multiple inferences in the time it takes a large model to run a single inference.
In modern decoder models, like the GPT family of models, they use autoregressive sampling, whereby to sample a sequence of N tokens, the model runs inference N times, each time consuming the result of the previous inference.
In speculative decoding, you run two models in parallel. The fast one runs a batch of inference and guesses which tokens the big model will predict. It compounds these guesses. In the meantime, the big model is running in the background, checking that the smaller model recorded the same results. The small model is able to make many guesses in the same time that the big model is able to make one. However, given that we have spare compute capacity, the big model is able to evaluate all of the guesses in parallel. As such, the only place where we pay the sequential cost of generating a sequence is for the smaller model.
The major disadvantage to speculative decoding is that it requires a “draft” model that is able to predict the output of the larger model, and you have to have both models in memory on the same machine (or on the same node in a multi-GPU setting). This adds complexity, and requires additional work, as you have to be training two models (the original one, and the “draft” one). Moreover, any performance benefits are limited by how accurately the smaller model is able to predict the larger one. If the smaller model was consistently able to predict the behaviour of the larger model, we’d just use it! Consequently, there’s a fundamental gap in how well speculative decoding can perform. HuggingFace has claimed that it typically doubles the decoding rate, which is consistent with the original paper, which claimed a 2x-3x improvement.
A technique recently came out which tries to improve on this by having the model generate n-grams, and recursively match them, without requiring a draft model. There’s a technique called Jacobi decoding (figure taken from their blog) which is a potential improvement over greedy decoding. How it works is that, at every point where you generate a token, you generate n tokens, making a “guess” as to the entire sequence. Then, you verify this against your previous guess; if the two match, then you accept the guess. This can enable latency improvements with no downside, as in the worse case, it devolves into greedy decoding.
Lookahead decoding improves on this further by keeping the n-grams that have been generate through the decoding process, and trying to use them as guesses. Given that there is a high correlation between the text that has been generated and the text that will be generated, this also has the possibility to improve latency dramatically, with minimal cost. It’s a very clever trick. I’m unaware of anyone using it, given how the technique was announced yesterday; very curious to see how it performs in real world scenarios.
Effective sparsity
In a decoder transformer, the beating heart of the model is the attention mechanism, summarized in the attention equation:
The softmax operation makes values that are not the max really small
:
Consequently, we are multiplying the values tensor (V in the attention equation) by a tensor that is mostly zeros. As a result, the output of the attention mechanism has a lot of zeros— up to 97% (h/t @yesthisislion). Similarly, after each ReLU in the MLPs, we also have a lot of sparsity.
Now, unfortunately, it’s kinda tough to actually make use of this. If we have sparsity in the weights, there’s a lot of work that can be done there through structured sparsity (e.g. torch.sparse), but it’s not actually clear how much current systems are able to make use of activation sparsity.
One optimization that can be done, is that if an activation is zero, you can just skip loading the weights that correspond to that activation, and skip the corresponding computation. This isn’t really supported in mainstream tensor programs as far as I can tell, but for a custom inference implementation, like, say, Llama.cpp has, it would be easy to implement.
The reason for this is that the activations are a function of each token, and thus, so too is the effective sparsity, causing it to be randomly distributed over the tokens. As a result, the effectiveness of this decays exponentially with batch size. If we have an effective sparsity of X% and a batch of size N, the likelihood that all entries for a given activation will be zero across the batch is given by X^N. I have a table for varying values of X and N. The decay is dramatic!
As a result, it’s tough to make use of this except in the batch size 1 regime, and even then, it’s typically more useful to use speculative decoding. But if you’re trying to run inference locally, and really need to get your latency down, this can be a great trick to use.
Quantization
Quantization is one of the better known tricks. I wrote about it before, so I’m not going to spend a ton of time on the actual methods. It’s tough to quantify how well quantization works. Much of the literature, such as the GPTQ paper, was done with models that aren’t close to SOTA, as the big labs aren’t publishing, and academics can’t match the resources that the big labs have.
For instance, GPTQ reported results quantizing the OPT & BLOOM models, which are much worse than the current crop of open source models, let alone GPT-4.
Of course, the big labs aren’t reporting what they’re doing, and most of the anecdotal reports I’ve seen are from people who are trying to run smaller models on consumer grade hardware, which is extremely memory limited. I think that a lot of hobbyists (i.e. people who don’t work as researchers at big labs) are blinded by the appeal of running a really big model locally, so they get really excited about quantization. But there’s no intrinsic advantage to quantization! From a first principles perspective, if you have two models that have the same number of bits, they should have the same number of tokens/s, and should have a similar level of performance. There would only be a big difference if we were doing a terrible job of using the bits in higher precision formats.
The literature doesn’t agree with my intuition— the aforementioned GPTQ paper found a negligible decrease in performance from quantizing models to up to 4x lower precision. I think that an explanation for this is that it’s much easier to quantize worse models without sacrificing performance. If we consider two identical LLMs, one trained with 2 trillion tokens, one trained on 500B tokens (call them LLM-2T, LLM-500B), I think we should expect the one trained with the higher number of tokens to suffer more when quantized, as it should be making better use of the tokens. We’d still expect the quantized LLM-2T to be better than LLM-500B, but I expect the performance decrease to be bigger from LLM-2T to quantized LLM-2T rather than LLM-500B to quantized LLM-500B.
Note: While I find the above argument compelling, it’s not at all supported by the literature. Quantizing does appear to be pretty darn close to a free lunch.
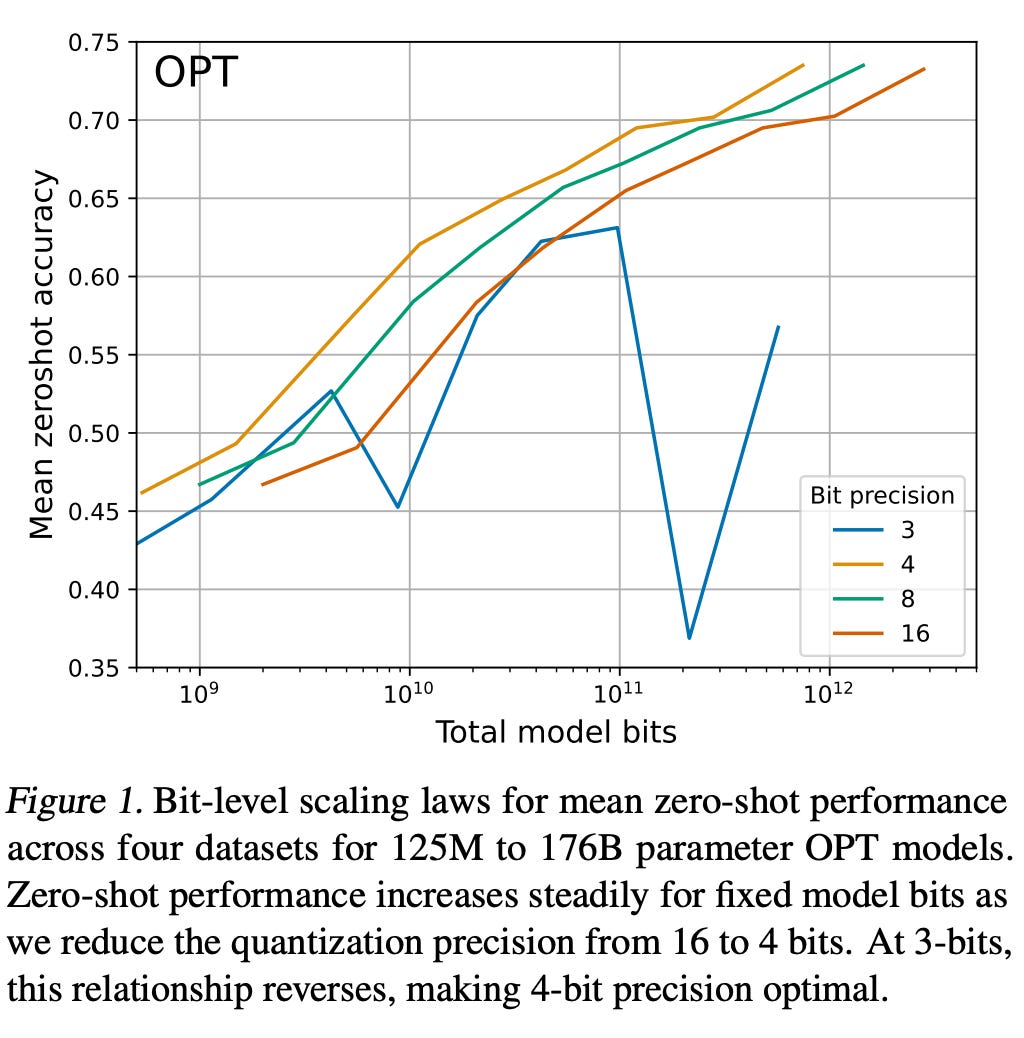
More recent work, like the *k*-bit inference scaling laws paper, ran an incredible number of experiments across a family of LLM architectures, reporting how allocating your bits differently affects performance. They studied the tradeoff between having a model with N parameters at a given level of precision vs having a model with 2N parameters and half the precision. Their results were pretty compelling, being almost indistinguishable from no penalty for quantizing (at least for 4 or more bits):
They found, basically, that you can go down to 4 bits without any penalty. There is almost no tradeoff from quantizing! You can run a 4x smaller model without a significant drop in performance. As inference performance on modern accelerators is equal to the number of bits you process (i.e. you can get Nx more operations per second when using Nx less precision), this is great.
My conclusion then, such as it is, is to use the recommendations from the k-bit inference paper. However, I’m hesitant to recommend using precision that’s lower than 8-bit for production workloads. fp8 is the lowest precision level floating point format that is supported natively by modern accelerators, and even then, support is limited. I would train and run inference in fp8, and see if the tradeoff in accuracy from quantizing further is acceptable for your usecase. I would struggle to recommend running a lower level of precision in a production environment when it doesn’t have native support from the platforms (i.e. Nvidia and the Torch/JAX teams).
As far as I can tell from the literature (which matches my intuition), fp8 is strictly better than int8, but it has limited support in hardware. If you’re at a GPU rich organization and get to use H100s for everything, use fp8. Otherwise, int8 is fine, and is much easier to use— PyTorch makes it quite easy (although the APIs are unstable).
When it comes to actually quantizing your model, the PyTorch team has a writeup of how to actually do this, and they provide a bunch of APIs to make it easy, although they’re unstable. bitsandbytes is another excellent library for quantization, although I haven’t used it personally.





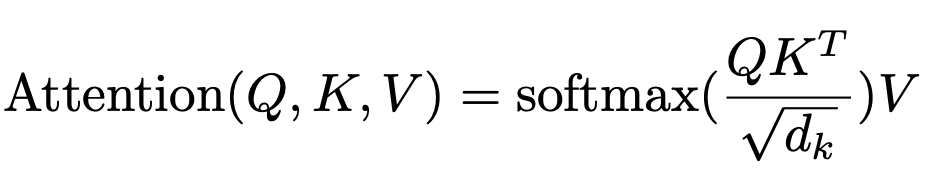



Quantization might work because LLMs are fairly noise resistant and can thus cope with the gaussian esque noise introduced by quantization fairly well
Thanks for writing.
I didn't see an explanation as to HOW the predictions from the smaller, faster model are incorporated into the predictions of the larger model, though, in the case of speculative decoding.